Egyszerű- és kamatos kamatszámítás

Az excelben hogyan lehet kiszámolni a kamatos kamatot? - kérdeztétek.
Minden - matematikai képlettel leírható - számítás megoldható. A számítást leíró képlet megfeleltetésére egy remek példa a kamatszámítás, legyen az egy egyszerű kamatszámítás vagy kamatos kamatszámítás. Ha ezt a megoldást sikerül megértened, akkor nem csak a kamatos kamatot tudod kiszámítani excelben a táblázatkezelő lehetőségével, de bármely más-, képlettel megadott számítást is el tudsz végezni, olvasd csak végig és próbáld ki a leírtakat. (utolsó módosítás: 2019.09.30.)
A kamatszámítás fogalmai
Megjegyzés: Fogalmakkal kell kezdenem, másként nincs rá módom leírni ezt a pénzügyi számítást, csakis a megfelelő pénzügyi fogalmakat használva.
Kamat - a pénz használata után - rendszerint évenként - fizetendő használati díj.
Kamatláb - a kamat mértékét százalékban megadó érték. pl ha az éves kamat 5% akkor az évi kamat a pénzösszeg 5%-a. Nem teljes évre ennek az összegnek, az idővel arányos része a kamat.
Jövőérték - az az összeg, amennyit a kezdőtőke ér a kamatozási időtartam végén. Egyszerű kamatszámításnál a kamatszámítási periódus végén - többnyire az év elteltével, a kamatot kiszámolják, ám a következő évi kamat alapja csakis a tőke összege, a kamat után nincs kamatszámítás. A kamatos kamatszámításnál a kamatszámítási periódus végén az alaptőkéhez hozzáadják a kamatot és a következő kamatszámítási periódusban a megnőtt tőke után számolják a kamatot, vagyis a kamat is kamatozik.
A példa kamatos kamatszámításra
példa a kamatos kamatszámításra, 15%-os kamattal:
| év | Év eleji tőke | Kamat | Évvégi tőke |
|---|---|---|---|
| 1. | 100 000 | 100 000 * 0.15 = 15 000 | 115 000 |
| 2. | 115 000 | 115 000 * 0.15 = 17 250 | 132 250 |
| 3. | 132 250 | 132 250 * 0.15 = 19 838 | 152 088 |
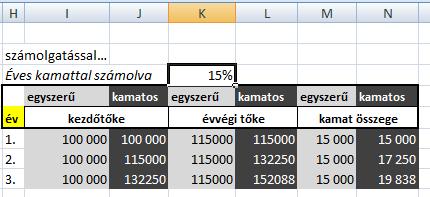 Kamatos kamat számolgatásEzt az aprólékos számítást persze nem célszerű csinálni! (a csatolmányból letölthető munkafüzetben a H3:N8 tartomány tartalmazza ezt a számítást) Helyette a következő képleteket alkalmazhatjuk:
Kamatos kamat számolgatásEzt az aprólékos számítást persze nem célszerű csinálni! (a csatolmányból letölthető munkafüzetben a H3:N8 tartomány tartalmazza ezt a számítást) Helyette a következő képleteket alkalmazhatjuk:
A kamatos kamatszámítás képletei
Két képletünk van, amelyek segítségével kiszámolhatjuk hogy adott kamat mellett, megadott futamidő végére a kiindulásnál meglévő tőkéből mennyi összegre számíthatunk és mennyi kamat keletkezik ez alatt a futamidő alatt.
Jövőérték a futamidő végére

Kamat összege a futamidő végére

A kamatláb alatt értjük azt az értéket, amely meghatározza a kamat százalékos nagyságát (pl 15 a kamatláb, akkor ez azt jelenti, hogy a kamat 15%, azaz 15/100 -a az alapnak)
Jövőérték számítása a munkafüzetben
A következőképpen célszerű eljárni a munkafüzetben:
- ForrásadatokVigyük fel a munkafüzetbe a forrásadatokat. A mellékelt munkafüzet a B2:B4 tartomány celláiba kerültek, balra a címkék.
- A forrás cellákat célszerű elnevezni a képlet egyszerűbb és áttekinthetőbb alkalmazásához. Figyelem: a névvel azonosított cella névvel abszolút cellahivatkozást lehet megvalósítani.
Az elnevezések a következők: B2 - x B3 - n B4 - kamat azaz a képletben szereplő p kamatláb 100-ad része. A képletben ezzel a cellatartalommal használjuk a képlet p/100 értékét. - A jövőértéket a munkafüzet C11-es cellába vittem be: =x*(1+kamat)^n
- A teljes futamidő kamatát kiszámoló képletet a C12 cellába vittem be: =x*((1+kamat)^n-1)
megjegyzés: a kamat tartalmat természetesen úgy is kiszámíthatjuk, hogy a kiszámolt jövőértékből levonjuk a kiinduló tőkét, de ezt már csak akkor tudjuk megtenni, ha a jövőértéket kiszámoltuk. Jól jöhet a képlet azonban akkor, ha csakis a kamatos kamat kamat összegére vagyunk kíváncsiak, csak ezt szeretnénk kiszámolni és a jövőértéket nem. Ezzel készen is vagyunk a kamatos kamat számításaival, csatolmányból letölthető excel munkafüzet tartalmazza a fogalmak magyarázatát és azokat a képeket is, amelyeket fentebb használtam.
Válljék kedves egészségetekre a használata :-) (sok-sok mindent részletezhettem volna még a feladat megoldásában, nagyon hosszúra nyújtaná az írást. Ha valamit nem értenétek, akkor itt a hozzászólásnál mondjátok el, köszönöm)
- Új hozzászólás

- 166771 olvasás

Hozzászólások
Napi kamatos kamat számítás
Napi kamatos kamat számításhoz szeretnék segítséget kérni.
befektettem 10$, melyre naponta kapok 3% hozamot(0.30$). A napi hozamot vissza tudom forgatni 20%-40%-60%-80%-100%-ban,és másnap már a hozammal növelt összegre adja a 3%-os hozamot.
Szeretném excelben/open office táblázatban kimutatni,hogy x napokon mennyi összeg áll rendelkezésemre. Olyan függvényre lenne szükségem,ahol a fix napi 3%-os kamat mellett: változtani tudom a tőkét változtatni tudom a visszaforgatás %-os arányát változtatni tudom a napok számát Jelenleg open office van a gépemen, és az excelt online tudom használni.
Ha lenne olyan függvény a fenti kamatos kamat példámra, ami mindkét esetben tudnám használni,azt nagyon megköszönném. Rengeteg cikket elolvastam már a témában,de konkrét megoldást nem találtam, és a függvények között nem igazán igazodok ki.
Előre is köszönöm a segítséget bunora
kamatos kamat számításához függvény
nem találtam fügvényt kamatos kamatszámításhoz sem, amit pedig leírtál, az még ettől bonyolultabb eset. ...ha jól értem, akkor a kamatos kamat számításánál, az előző periódusban elért kamatnak csak egy megadott százaléka kamatozik tovább.
A fenti képlet sem megfelelő ennek kiszámítására, úgy gondolom erre egyedül egy makró írása adhatna megoldást.
...egyik napról a másikra viszont képlettel meghatározható az elért kamat összeg. Ha megfelelően állítod össze a képletet, akkor az másolható, így egy lista hozható létre, amelyből kiolvasható pl a 10. sorból a 10. nap után járó kamat. Ez persze jó kis favágó munka is egyben, ám ha megoldod, akkor már belefoghatsz a makró elkészítésébe is, a forrás adatokat cellákban rögzítve, hozzá egy ikonnal indítható módon hozzárendelve a makró.
Az online kamatos kamatszámítás kalkulátorok között is lehetne helye, ha ez a probléma mások számára is ad megoldás, ha a problémád egy létező probléma és nem egy vizsgafeladat csupán.