Egyenletrendszer megoldása Excellel

Egyenletrendszer megoldása Excellel - lépésről-lépésre, s ha Excel, akkor máris indítsd a táblázatkezelődet, hogy végigcsináld velem.
Egyenletrendszer, értsd alatta a lineáris egyenletrendszert
A lineáris egyenletrendszer főbb ismérvei:
- ahány ismeretlen, annyi egyenlet írja le . Ha az ismeretleneket jelöljük az a, b, c, d betűkkel, ez azt jelenti, hogy 4 ismeretlenünk és 4 egyenletünk van, pl.:
5a - 1b + 7c + 5d = 3
4a - 4b + 7c - 2d = 1
5a + 6b + 8c + 3d = -1
3a + 7b + 4d = 9 - Az ismeretlenek minden egyenletben - az egyeletrendszer egyenleteinek baloldalán -, bírnak együtthatóval. Ez az a szám, amely az ismeretlen szorzójaként, előtte látható.
- Ezek az együtthatók adják ki az úgynevezett együttható mátrixot.
- Ennek az együttható mátrixnak annyi sora van, ahány egyenlet, annyi sora, ahány ismeretlen. A lineáris egyenletrendszerben - mint amilyen a példánk is - ez a két érték egyenlő;
pl. az első egyenletünkben az a együtthatója az 5, a b együtthatója -1, a c együtthatója 7 és végül a d együtthatója 5
--- a negyedik egyenletben a c együtthatója a 0 - azaz a nulla.
...az együtthatók adják ki az együttható mátrixot. - az egyenletek egyenlőségjelétől jobbra van az eredmény. Ezek az eredmények - konstansok - alkotják az eredmény vektort :-( bocs
Az egyenletrendszer megoldása Excellel - 1.lépés adatatok rögzítése a számításhoz, a munkafüzetben
Mint minden feladat megoldásánál az Excelben, felvisszük az adatokat a számításokhoz, majd csak ezt követően jöhetnek a számítások. A feladat megoldásának ugyanúgy, ahogy az adatok bevitelét, a különleges forma határozza meg.
Együttható mátrix - az egyenletrendszer megoldása Excellel
Konkrét példánkban 4 db egyenletünk van, ez azt jelenti, hogy az együttható mátrix:
- 4 oszlopa lesz,
- 4 sora.
- Az 1. oszlopban az első ismeretlen, azaz az a együtthatói, az 5, 4, 5, 3
- A 2. oszlopban a második ismeretlen, azaz a b együtthatói, a -1, -4, 6, 7
- A 3. oszlopban a harmadik ismeretlen, azaz a c együtthatói, a 7, 7, 8, és 0 Figyelem, fontos: a negyedik egyenletben nem szerepel a harmadik ismeretlen, ez számunkra azt jelenti az adatok bevitelénél, hogy az Ő együtthatója 0, azaz nulla. Az együttható mátrixban minden sorban/oszlopban minden ismeretlennek van együtthatója! A mátrixnak teljesnek kell lennie, azaz nem lehet rövidebb sora vagy oszlopa!
- A 4. oszlopban a negyedik ismeretlen, azaz a d együtthatói, az 5, -2, 3, 4
(alább kapsz egy ábrát a további egyeztetéshez, fontos hogy értsd az együttható mátrixot!)
1. lépés: Vigyük fel az együttható mátrixot és az eredmény vektort, lássuk az egyenletrendszer példánkat:
Az alábbi ábrán a bevitt együttható mátrixot láthatod A1 cellától D4 celláig:
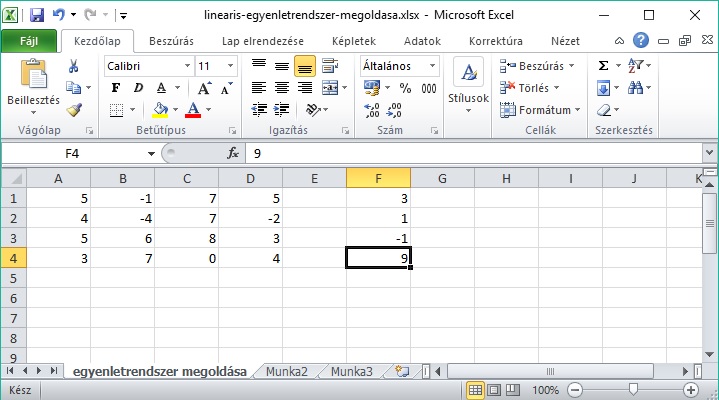
Ezzel elkészült az együttható mátrix, jöjjön az eredményvektor, a számításhoz szükséges másik igen fontos adat halamaz! (az ábrán láthatod már az eredmény vektort is)
Eredményvektor - az egyenletrendszer megoldása Excellel
Az egyenletrendszer egyenleteinek jobboldalán értékek szerepelnek - ők adják az eredmény vektort.
A vektornak egy oszlopa van és több sora, konkrét példánkban 4. Vektor lenne akkor is ha lenne 1 sora és 4 oszlopa! Most viszont az eredménynek a sor végén kell lennie, az egyenletek sorait vittük fel sorokba, ezért az egyes soroknak megfelelő eredményt visszük az együttható mátrixal összhangban, annak soraival egy sorba.
Az eredmény vektor értékei, az egyenletek jobb oldaláról 3, 1, -1 és 9.
A fenti ábrán látható módon vidd fel Te is az eredmény vektort, tehát a mátrix sorainak folytatásában, ám egy üres oszlop maradjon ki, az együttható mátrix és az eredmény vektor tartománya között:
2.lépés: vigyük be az F1-F4 tartományba az egyenletek jobb oldalán szereplő összegeket, sorban a 3, 1, -1 és 9 értékeket, azaz az eredmény vektort!
A fenti ábrán ellenőrizheted ennek a bevitelét is, feltétlenül ellenőrizd az előjeleket is! A + jelet nem kell bevinni, a nélkül is pozitív lesz a bevitt érték, ám a minusz jelet feltétlenül vidd be!
Egyenletrendszer megoldása Excellel - a tényleges számítás!
Mit is szeretnénk megkapni a számításunk eredményeként? A négy ismeretlen a, b, c, d értékét! Ez azt jelenti, hogy 4 cellára van szükség az eredményhez :-)
4. lépés: Jelöld ki azt a tartományt - pl H1-H4 - azaz legyen pont akkora mint az eredményvektor és pont annyi cella, ahány eredményt várunk -, és ott ahol szeretnénk az eredményt látni. Szemléletesebb lesz az eredmény - én azért vittem a H oszlopba
5. lépés: Kattints a képlet beviteléhez a Szerkesztőlécbe, majd kattints az egyenlet bevitelére szolgáló gombon. Válaszd ki az MSZORZAT() függvényt!
a Mat. trigonom. kategóriában találod. A függvény kiválasztásánál olvasd el a függvény működéséről szóló leírást is.
(a függvényt a Mátrix kategóriában találod, ha nem ismernéd a mátrix függvényeket, akkor egy másik írásban olvashatsz róla részletesen)
- Az MSZORZAT() függvény két paraméterét vigyük be!
Az első tömb Tömb1 - legyen az együttható mátrix inverze, amelyet az INVERZ.MÁTRIX()-l készítünk el. Tehát kattints az MSZORZAT Tömb1 mezőjébe, majd a függvény beszúrása gombon, a Szerkesztő léc mellett. Itt válaszd ki az INVERZ.MÁTRIX függvényt. Ennek a függvénynek csak egyetlen bemenő paramétere van, idekattintva mutasd meg az együttható mátrixot, azaz az A1-D4 tartományt. - Most kellene visszalépni az MSZORZAT függvény paneljéhez. Ezt úgy tesszük meg, hogy a Szerkesztőlécben belekattintunk a függvénybe. Ennek a kattintásnak az eredményeként megjelenik az MSZORZAT panelje, a Tömb1-ben látható az imént felvitt inverz függvény.
- Az MSZORZAT() függvény Tömb2 paraméteréhez vigyük be az eredményvektort, azaz az F1-F4 tartományt. Most így néz ki a függvény panelje, NE kattints még a Kész gombra:
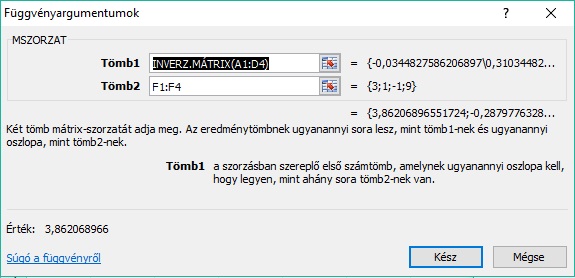
- Készen vagyunk a képlettel, ám ezt tömb/mátrix módjára kell lezárni. Üsd le a Ctrl + Shift + Enter billentyűkombinációt. Az eredmény így néz ki:
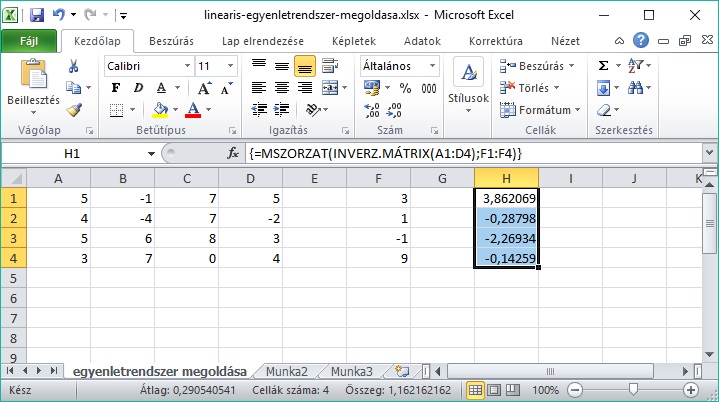
A képlet kapcsos zárójel közé került. Ha módosítani kellene, akkor a módosítás alatt eltűnnek a kapcsos záróljelek, de ne feledd, a végén a Ctrl + Shift + Enter billentyűkombinációval zárd le, ismét.
Az eredmény tetszés szerint formázhatjuk! Ha csökkentjük a tizedesjegyek számát, akkor kerekítést kapunk a cellában látható értékre(a cellában a legnagyobb pontossággal van az érték, csak a megjelenő értékről beszélünk!)
Ellenőrizd a megoldás helyességét, azaz az eredeti egyenletrendszerbe helyettesítve a kapott értékeket, az egyenletek jobboldalán szereplő értékeket kell kapni!
Maradt nyitva kérdés? Tedd fel hozzászólásodban, ha kell, akkor töltsd le alább azt az excel munkafüzetet, amelyben én dolgoztam.
Külön köszönet Knausz Lajosnak, a probléma felvetéséért, a megoldandó egyenletrendszer tőle származik :-)
| Csatolmány | Méret |
|---|---|
| 8.84 KB | |
| 12.92 KB |
- Új hozzászólás

- 7533 olvasás
